Hello friend, and welcome back to How to Learn Machine Learning!
In this article, we’re diving into one of the most fascinating—and often misunderstood—areas of modern Machine Learning: Manifold Learning.
If you’ve ever wondered how algorithms “unwrap” complex, high-dimensional data into meaningful low-dimensional structures… you’re about to find out!
1. Introduction: What Is Manifold Learning?
We live in a world full of high-dimensional data: images, sounds, text embeddings, sensor readings, gene sequences—everywhere you look, the dimensions explode.
But here’s a secret: Even though the data lives in high-dimensional space, its true structure is often low-dimensional.
This low-dimensional structure is called a manifold, and manifold learning refers to the set of algorithms that try to uncover this hidden structure.
Think of it like:
- Flattening a crumpled sheet of paper
- Unfolding a Swiss roll
- Discovering that a huge dataset really lies on a simple curve or surface
Manifold learning is a cornerstone technique in ML for:
- Dimensionality reduction
- Visualization
- Preprocessing for clustering or classification
- Understanding embeddings in Deep Learning
It’s math, geometry, and intuition all mixed together—ML magic.
2. Why Manifold Learning Matters
Manifold learning allows us to do many things. Here we will list the most important ones.
2.1. Visualize Data in 2D or 3D
Tools like t-SNE and UMAP help reveal clusters, anomalies, and relationships.
2.2. Improve Model Performance
Reducing dimensions removes noise and focuses models on the variables that matter.
As with other Dim reduction techniques, specially useful for models that calculate some sort of distance metric, Manifold Learning allow us to reduce noise and simplify the models.
2.3. Discover Hidden Structure
High-dimensional data rarely lies everywhere. Manifold learning finds where the structure actually is.
2. 4. Power Deep Learning Embeddings
Word embeddings (find super cool article here), image embeddings, and latent spaces are all built on manifold ideas.
3. Popular Manifold Learning Algorithms
Principal Component Analysis (PCA)
Yes, PCA counts! The most famous dimensionality reduction algorithm by excellence. Taught in all DS or AI courses, consisting on extracting the eigenvectors and eigenvalues of our data, that is, the directions of most change.
It assumes the data lies on a linear subspace (a flat manifold).
Great for speed, okay for complex, nonlinear structure.
3.2 Isomap
Captures geodesic distances—the distances along the manifold.
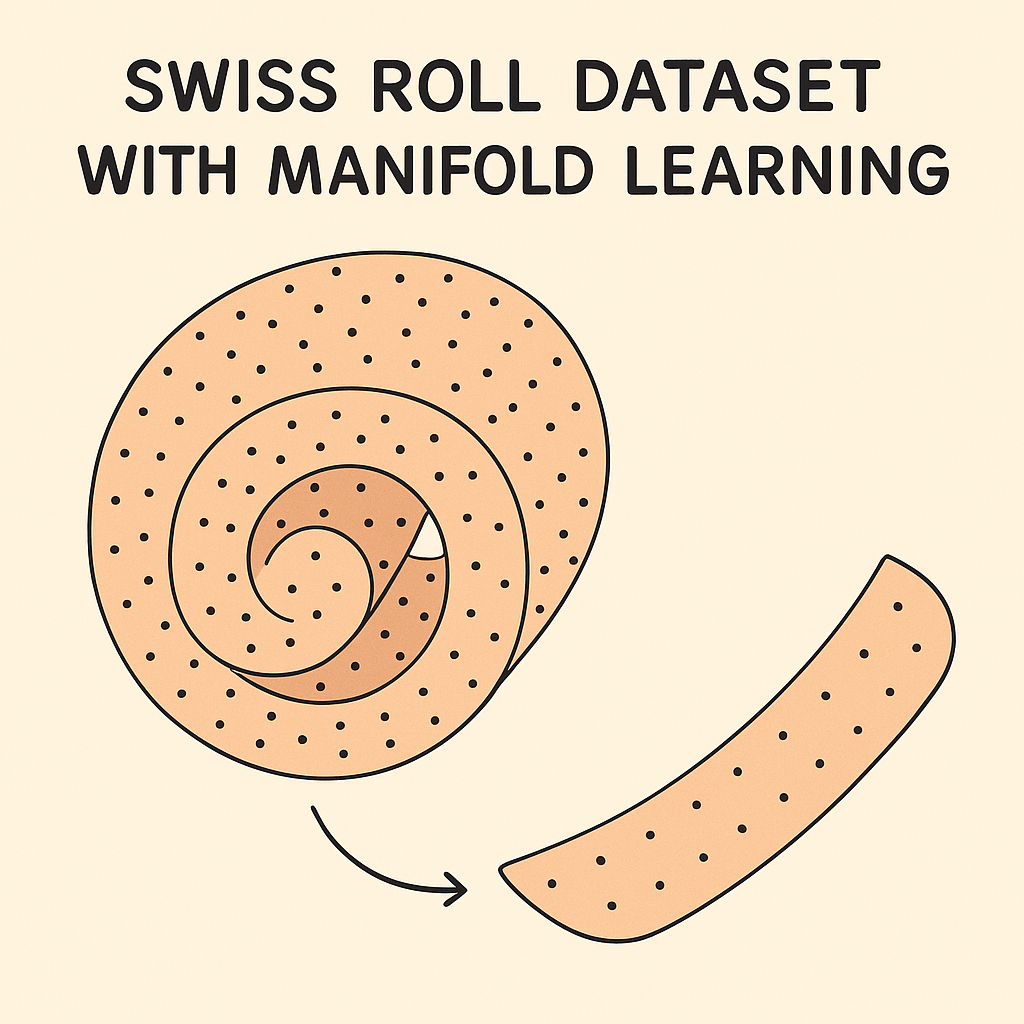
Perfect for “unfolding” curved surfaces like the famous Swiss roll dataset.
3.3 Locally Linear Embedding (LLE)
LLE assumes that each small neighborhood of points is approximately flat.
It preserves local relationships, making it great for:
- Motion data
- Sensor data
- Face images with varying pose
3.4 t-SNE
The king of visualizations. I don’t really love it because aside from visualizing its not great for anything else – In a traditional ML pipeline you will most likely use PCA to reduce Dims, and not t-SNE.
Turns high-dimensional distances into probabilities and reveals clusters beautifully. A word of Caution: t-SNE is not good for global structure, but great for clusters.
3.5 UMAP (Uniform Manifold Approximation and Projection)
A more modern alternative to t-SNE:
- Faster
- Better global structure
- Excellent for embedding exploration
UMAP is widely used in NLP, bioinformatics, and deep learning interpretability. Much preferred.
4. Real-World Applications of Manifold Learning
Bioinformatics
Analyzing gene expressions, cell transcription states, and other high-dimensional biological signals.
Deep Learning
Understanding latent spaces in autoencoders, GANs, and diffusion models.
Image Recognition
Faces under different lighting conditions lie on smooth manifolds—perfect for manifold methods.
Speech Processing
Vocal tract configurations form low-dimensional shapes, even if the raw audio looks high-dimensional.
5. A Simple Intuition: The Swiss Roll Story
Imagine taking a long strip of paper and rolling it up into a spiral.
Although the data appears complex in 3D, the true structure is just a 2D sheet.
Manifold learning algorithms try to:
👉 Recover the original 2D sheet without tearing or stretching it.
This is the heart of manifold learning.
Some Cool links here
Summary: Why You Should Care About Manifold Learning
Manifold Learning is the bridge between raw high-dimensional chaos and beautifully organized low-dimensional structure. Whether you’re visualizing embeddings, uncovering hidden patterns, or preprocessing data for your models…
Manifold Learning reveals the true geometry of your dataset.
It’s powerful, elegant, and surprisingly intuitive once you see it in action.
As always thank you so much for reading How to Learn Machine Learning, and have a wonderful day!
Subscribe to our awesome newsletter to get the best content on your journey to learn Machine Learning, including some exclusive free goodies!

